
今回は、円柱の体積の求め方(公式)について書いていきたいと思います。
円柱の体積の求め方【公式】
円柱の体積は、次の公式で求められます。

円柱の体積=底面積×高さ
底面積は円の面積。
円柱の体積を求めるときには、底面積である円の面積に円柱の高さをかけると覚えておくといいでしょう。⇒ 円の面積の求め方
スポンサードリンク
円柱の体積を求める問題
では実際に円柱の体積を求める問題を解いていきたいと思います。
問題①
次の円柱の体積を求めましょう。
(円周率は3.14とします。)
《円柱の体積の求め方》

この円柱の底面は、半径が8cmの円なので
底面積=8×8×3.14=200.96(㎠)
求める円柱の体積=底面積×高さ=200.96×10=2009.6(cm³)
答え 2009.6cm³
問題②
次の円柱の体積を求めましょう。
(円周率は3.14とします。)
《円柱の体積の求め方》

円柱の体積=底面積×高さなので
求める円柱の体積=3×3×3.14×7=197.82(cm³)
答え 197.82cm³
スポンサードリンク
問題③
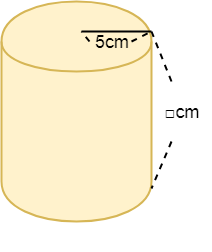
体積が628cm³である次の円柱の高さを求めましょう。
(円周率は3.14とします。)
《円柱の高さの求め方》
円柱の体積=底面積×高さであることから
円柱の高さ=円柱の体積÷底面積で求めることができます。
ここで底面積=5×5×3.14=78.5
よって、円柱の高さ=628÷78.5=8(cm)となります。
答え 8cm
問題④
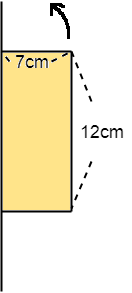
棒に長方形の1辺が次のような形でついています。
長方形の1辺がついた部分を軸として棒を回転させると、どのような立体ができますか。
またその立体の体積を求めましょう。(円周率は3.14とします。)
《立体の体積の求め方》
長方形の1辺がついた状態で棒を軸として回転させると、下の図からもわかるように円柱になります。

この円柱は半径7cmの円が底面、高さが12cmなので
円柱の体積=7×7×3.14×12=1846.32(cm³)となります。
答え 円柱ができる。体積は1846.32cm³
~立体の体積・表面積を求める公式まとめ~
スタディサプリ/塾平均より年間24万円お得!? 月額980円(税抜)/テキスト代無料 ![]()
スポンサーリンク
こちらもどうぞ。